- 全國統一銷售熱線:
- 北京總部:
- 010-64437473
- 上海:
- 021-62113795
- 深圳:
- 0755-86241216
高壓水射流壓力釋放效應的理論分析和壓力計算
時間:2012-11-29 來源: http://www.quanjingst.com
卸載和加載一樣可以使受載物料發生破壞。同樣,顆粒在液體的靜水壓力作用下,由于彈性變形而體積縮小,并在顆粒中儲存彈性應變能。當壓力突然釋放時,儲存在顆粒中的應變能會隨之釋放。由于材料的抗拉強度遠遠低于其抗壓強度,而且應變能的突然釋放和慣性作用就會導致顆粒卸載時的拉應力破壞。
在高壓水射流粉碎中,物料顆粒被加入到水射流中,首先顆粒受到靜水壓力被加壓到高壓狀態,使得顆粒內儲存有很高的彈性應變能,然后經水射流加速而被突然釋放,實現壓力釋放效應而被粉碎。
對于突然卸載的載荷釋放效應,我們可以通過簡單的彈簧加卸載過程來說明。
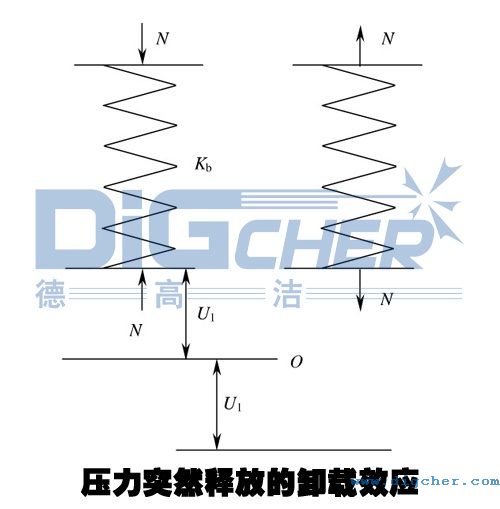
上圖所示的彈簧,其剛度為 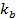 ,當作用在其上的力增大到 N 時,彈簧端部被壓縮到
,當作用在其上的力增大到 N 時,彈簧端部被壓縮到 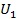 ,而相應彈簧的壓縮應變能為
,而相應彈簧的壓縮應變能為 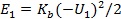 。此時如果將作用力 N 突然移去,彈簧立即下彈,并發生振動。由于能量守恒,其下端瞬間最大位移可達平衡位置 O 點以下的
。此時如果將作用力 N 突然移去,彈簧立即下彈,并發生振動。由于能量守恒,其下端瞬間最大位移可達平衡位置 O 點以下的 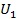 處。也就是說突然卸載的載荷效應,相當于將量值相同的荷載,反向加到其上。
處。也就是說突然卸載的載荷效應,相當于將量值相同的荷載,反向加到其上。
與原加載不同的是,加載時彈簧承受的是壓應力,而卸載時彈簧承受的是拉應力。對于抗拉強度低于其抗壓強度的材料,采用壓力釋放進行粉碎是完全可行的。實際上,大多數脆性材料都具有抗拉強度遠遠低于其抗壓強度的特性。
根據斷裂力學可知,固體顆粒在外力作用下,其彈性應變能不斷增加,達到一定程度后,就在顆粒內形成裂紋或使裂紋不斷擴展,進而失穩破裂。其裂紋產生和擴展的能量全部來自于顆粒內儲存的彈性應變能。
假設被粉碎的物料顆粒為各向同性均勻球,球的半徑為 b,在球外表面受均勻壓力 p 的作用。由球對稱問題的平衡微分方程:
可以解得顆粒受到的應力表達式為:
在壓力作用下的應變為:
則顆粒在壓力 p 作用下的應變能為:
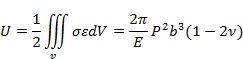 公式(7)
公式(7)根據破碎力學研究超細磨礦時,將破碎能定義為:輸入到球形顆粒上達到瞬時破碎的彈性應變能。并推導得出單位質量破碎能與強度的關系為:
對于半徑為 b 的球形顆粒:
代入公式(8)可得:
當顆粒受到均勻壓力 p 后,在其體內已聚集了如公式(7)所示的彈性應變能。如果將均勻壓力 p 突然釋放,則球體內將出現拉伸應力。因此,顆粒所受的應力只要達到材料的拉伸強度就會被破壞。所以,公式(10)的強度 S 就可用材料的拉伸強度 σl 來代替,則公式(10)可變為:
設積聚在顆粒內的彈性變形能,在釋放時全部轉變為顆粒的破碎能:
即:
公式(12)說明顆粒在壓力突然釋放時得到破壞,需給予球形顆粒的均勻壓力 p 的表達式。
如果考慮強度隨體積的變換,則給出的強度關系為:
即:
上式中,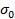 —單位體積試樣
—單位體積試樣 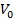 的拉伸強度;
的拉伸強度;
m —材料的均勻性系數。
公式(14)表明,要使半徑為 b 的球形顆粒受壓釋放粉碎所需的壓力,只與顆粒材料的物理力學特性和幾何尺寸有關。
由此可知,通過壓力釋放粉碎物理所需的壓力比材料的抗拉強度高,但要比材料的抗壓強度低很多。同時,作用在顆粒上的均勻壓力越大,積聚在顆粒內的彈性應變能就越高,壓力釋放后的粉碎效果就越好。
上一篇:壓力改變對超高壓水射流參數的影響
下一篇:壓力釋放效應的實驗研究
- 標簽:
- 理論分析
- 壓力計算
- 高壓水射流
- 壓力釋放效應
有效提高噴嘴壽命的幾個方法
2017-08-14
高壓清洗機清洗機理分析之最大清洗寬度的
2012-09-18
高壓水射流最大打擊力實測
2013-05-03
高壓清洗機進水腔密封失效的原因分析
2013-06-29
高壓清洗機高壓膠管段壓力損失理論分析
2012-07-06
高壓清洗機日常維護:噴嘴的磨損因素及更
2018-08-22
高壓水去毛刺機專用噴嘴介紹
2018-07-16
高壓水射流破碎混凝土的優點
2018-07-04
高壓清洗機在管道清洗時的注意事項
2018-06-28
高壓水射流清洗安全注意事項
2018-06-20



